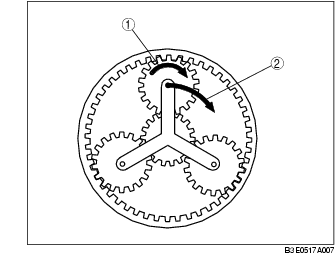
PLANETARY GEAR OPERATION
D6E051719540A03
• The planetary gear works as a transaxle when the sun gear and the internal gear are engaged.
• The sun gear, installed inside of the pinion gears, and the internal gear, installed outside of the pinion gears, are engaged with their respective gears.
The sun gear and the internal gear rotate on the center of the planetary gear.
|
1
|
Sun gear
|
|
2
|
Internal gear
|
|
3
|
Planetary carrier
|
|
4
|
Pinion gear
|
• The pinion gears turn in the following two ways:
-
- On their own centers (rotation)
-
- On the center of the planetary gear (revolution)
Gear ratio of each range
• The relation between each element of the planetary gear set and the rotation speed is generally indicated in the formula below.
(ZR+ZS) NC=ZRNR+ZSNS: formula (1)
In this formula Z stands for the number of teeth, N stands for the rotation speed, and R, S, C stand for each gear element (refer to the table below).
|
1
|
Sun gear
|
|
2
|
Internal gear
|
|
3
|
Planetary carrier
|
|
4
|
Pinion gear
|
Number of teeth and symbol of each gear
|
Planetary gear unit
|
Planetary gear element
|
Number of teeth
|
Unit identification symbol
|
|
Gear element
|
Unit
|
|
Front
|
Internal gear
|
89
|
R
|
F
|
|
Planetary carrier
(part of pinion gear)
|
20
|
C
|
F
|
|
Sun gear
|
49
|
S
|
F
|
|
Rear
|
Internal gear
|
98
|
R
|
R
|
|
Planetary carrier
(part of pinion gear)
|
30
|
C
|
R
|
|
Sun gear
|
37
|
S
|
R
|
|
Secondary
|
Internal gear
|
89
|
R
|
S
|
|
Planetary carrier
(part of pinion gear)
|
29
|
C
|
S
|
|
Sun gear
|
31
|
S
|
S
|
First gear
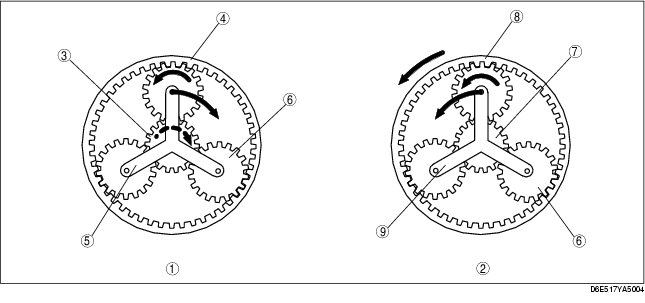
.
|
1
|
Front planetary gear
|
|
2
|
Secondary planetary gear
|
|
3
|
Sun gear NSF (input)
|
|
4
|
Internal gear (fix)
|
|
5
|
Planetary carrier NCF (output)
|
|
6
|
Pinion gear
|
|
7
|
Sun gear (fix)
|
|
8
|
Internal gear NRS (input)
|
|
9
|
Planetary carrier NCS (output)
|
Gear rotation speed
|
Planetary gear unit
|
Front
|
Secondary
|
|
Internal gear
|
0 (fix)
|
NRS (input)
|
|
Planetary carrier
|
NCF (output)
|
NCS (output)
|
|
Sun gear
|
NSF (input)
|
0 (fix)
|
• Suppose the reduction ratio on the main shifting side is i1,
i1=NSF/NCF.
• From the result NRF=0 in formula (1), the rotation speed of the front planetary gear unit can be calculated using the following formula:
(ZRF+ZSF)NCF=ZSFNSF
Therefore,
i1=NSF/NCF=(ZRF+ZSF)/ZSF=(89+49)/49=2.8163.
• Because the reduction ratio on the main shifting side is transmitted from the primary gear to the secondary gear, it can be calculated using the following formula:
The reduction ratio of the primary/secondary gear A = the number of primary gear teeth/the number of secondary gear teeth
Therefore,
A=82/86=0.9535
• Suppose the reduction ratio on the sub-shifting side is ii1,
ii1=NRS/NCS.
• From the result NSS=0 in formula (1), the rotation speed of the secondary planetary gear unit can be calculated using the following formula.
(ZRS+ZSS)NCS=ZSSNRS
Therefore,
ii1=NRS/NCS=(ZRS+ZSS)/ZRS=(89+31)/89=1.3483
And the reduction ratio of 1st gear= i1 x A x ii1=2.8163 x 0.9535 x 1.3483=3.620
As a result, the reduction ratio of 1st gear is 3.620.
Second gear
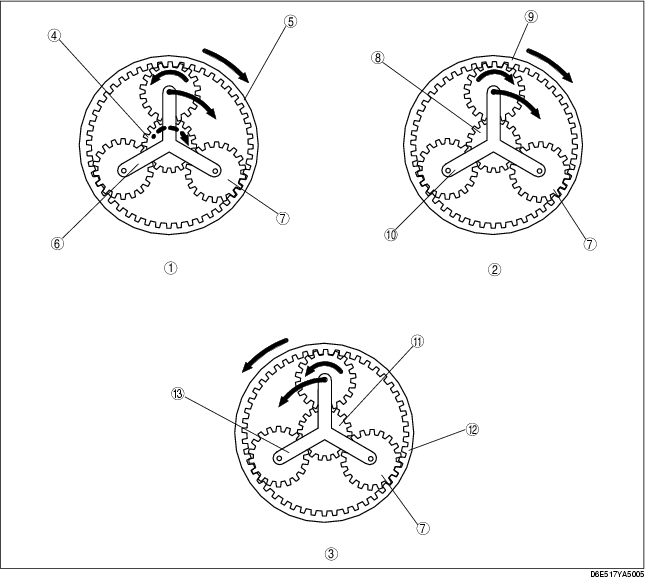
.
|
1
|
Front planetary gear
|
|
2
|
Rear planetary gear
|
|
3
|
Secondary planetary gear
|
|
4
|
Sun gear NSF (input)
|
|
5
|
Internal gear NRF=NC
|
|
6
|
Planetary carrier NCF (output) =NR
|
|
7
|
Pinion gear
|
|
8
|
Sun gear (fix)
|
|
9
|
Internal gear NRR (output) =NR
|
|
10
|
Planetary carrier NCR=NC
|
|
11
|
Sun gear (fix)
|
|
12
|
Internal gear NRS (input)
|
|
13
|
Planetary carrier NCS (output)
|
Gear rotation speed
|
Planetary gear
|
Front
|
Rear
|
Secondary
|
|
Internal gear
|
NRF=NC
|
NRR (output) =NR
|
NRS (input)
|
|
Planetary carrier
|
NCF (output) =NR
|
NCR=NC
|
NCS (output)
|
|
Sun gear
|
NSF (input)
|
0 (fix)
|
0 (fix)
|
-
Note
-
• The front internal gear and the rear planetary carrier are integrated.
-
• The front planetary carrier and the rear internal gear rotate at the same speed.
• Suppose the reduction ratio on the main shifting side is i2,
i2=NSF/NR.
• From formula (1), the relation between the gear ratio in second gear and the rotation speeds of the front and the rear planetary gar sets is indicated in formulas (2) and (3).
(ZRF+ZSF) NR=ZRFNC+ZSFNSF: (2) (Front planetary gear set)
(ZRR+ZSR) NC=ZRRNR+ZSRNSF: (3) (Rear planetary gear set)
• From the result NSR=0 in formula (3).
NC= (ZRR/ (ZRR+ZSR)) NR: (4)
• Here we substitute formula (4) in formula (2).
ZSRNSF= (((ZRR+ZSR) (ZRF+ZSF) -ZRFZRR) / (ZRR+ZSR)) NR
Therefore,
i2=NSF/NR= (((ZRR+ZSR) (ZRF+ZSF) -ZRFZRR) / (ZSF (ZRR+ZSR))) NR
= ((98+37)(89+49) -89 x 98) / (49 (98+37)) =1.4978
• Because the reduction ratio on the main shifting side is transmitted from the primary gear to the secondary gear, it can be calculated using the following formula:
The reduction ratio of the primary/secondary gear A = the number of primary gear teeth/the number of secondary gear teeth
Therefore,
A=82/86=0.9535
• Suppose the reduction ratio on the sub-shifting side is ii2,
ii2=NRS/NCS.
• From the result NSS=0 in formula (1), the rotation speed of the secondary planetary gear unit can be calculated using the following formula.
(ZRS+ZSS)NCS=ZSSNRS
Therefore,
ii2=NRS/NCS=(ZRS+ZSS)/ZRS=(89+31)/89=1.3483
And the reduction ratio of 2nd gear= i2 x A x ii2=1.4978 x 0.9535 x 1.3483=1.925
As a result, the reduction ratio of 2nd gear is 1.925.
Third gear

.
|
1
|
Front planetary gear
|
|
2
|
Secondary planetary gear
|
|
3
|
Sun gear NSF (input)
|
|
4
|
Internal gear NRF (input)
|
|
5
|
Planetary carrier NCF (output)
|
|
6
|
Pinion gear
|
|
7
|
Sun gear (fix)
|
|
8
|
Internal gear NRS (input)
|
|
9
|
Planetary carrier NCS (output)
|
Gear rotation speed
|
Planetary gear
|
Front
|
Secondary
|
|
Internal gear
|
NRF (input)
|
NRS (input)
|
|
Planetary carrier
|
NCF (output)
|
NCS (output)
|
|
Sun gear
|
NSF (input)
|
0 (fix)
|
• Here we have the result on NRF=NSF.
• Suppose the reduction ratio on the main shifting side is i3,
i3=NSF/NCF.
• From the result of NRF=NSF in formula (1), the relation between the gear ratio in 3rd gear and the rotation speed of the front planetary gar set is indicated in the following formula:
(NRF+ZSF) NCF= (ZRF+ZSF) NRF
Therefore,
i3=NRF/NCF= (ZRF+ZSF) / (ZRF+ZSF) = (89+49) / (89+49) =1.000
• Because the reduction ratio on the main shifting side is transmitted from the primary gear to the secondary gear, it can be calculated using the following formula:
The reduction ratio of the primary/secondary gear A = the number of primary gear teeth/the number of secondary gear teeth
Therefore,
A=82/86=0.9535
• Suppose the reduction ratio on the sub-shifting side is ii3,
ii3=NRS/NCS.
• From the result NSS=0 in formula (1), the rotation speed of the secondary planetary gear unit can be calculated using the following formula.
(ZRS+ZSS)NCS=ZSSNRS
Therefore,
ii3=NRS/NCS=(ZRS+ZSS)/ZRS=(89+31)/89=1.3483
And the reduction ratio of 3rd gear= i3 x A x ii3=1.000 x 0.9535 x 1.3483=1.285
As a result, the reduction ratio of 3rd gear is 1.285.
Fourth gear
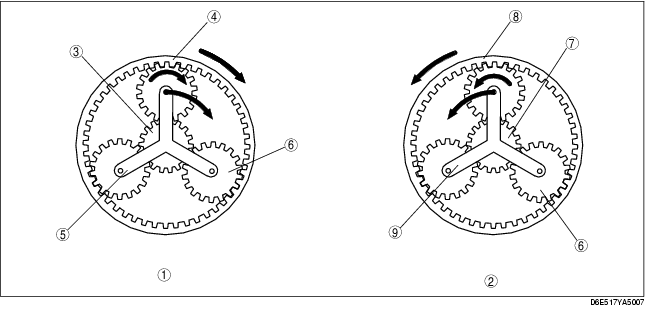
.
|
1
|
Rear planetary gear
|
|
2
|
Secondary planetary gear
|
|
3
|
Sun gear (fix)
|
|
4
|
Internal gear NRR (output)
|
|
5
|
Planetary carrier NCR (input)
|
|
6
|
Pinion gear
|
|
7
|
Sun gear (fix)
|
|
8
|
Internal gear NRS (input)
|
|
9
|
Planetary carrier NCS (output)
|
Gear rotation speed
|
Planetary gear
|
Rear
|
Secondary
|
|
Internal gear
|
NRR (output)
|
NRS (input)
|
|
Planetary carrier
|
NCR (input)
|
NCS (output)
|
|
Sun gear
|
0 (fix)
|
0 (fix)
|
• Suppose gear ratio in fourth gear is i4,
i4=NCR/NRR
• From the result of NSR=0 in formula (2), the relation between the gear ratio in fourth gear and the rotation speed of the rear planetary gear set is indicated in the following formula:
(ZRR+ZSR) NCR=ZRRNRR
Therefore,
i4=NCR/NRR=ZRR/ (ZRR+ZSR) =98/ (98+37) =0.7259
• Because the reduction ratio on the main shifting side is transmitted from the primary gear to the secondary gear, it can be calculated using the following formula:
The reduction ratio of the primary/secondary gear A = the number of primary gear teeth/the number of secondary gear teeth
Therefore,
A=82/86=0.9535
• Suppose the reduction ratio on the sub-shifting side is ii4,
ii4=NRS/NCS.
• From the result NSS=0 in formula (1), the rotation speed of the secondary planetary gear unit can be calculated using the following formula.
(ZRS+ZSS)NCS=ZSSNRS
Therefore,
ii4=NRS/NCS=(ZRS+ZSS)/ZRS=(89+31)/89=1.3483
And the reduction ratio of 4th gear= i4 x A x ii4=0.7259 x 0.9535 x 1.3483=0.933
As a result, the reduction ratio of 4th gear is 0.933.
Fifth gear
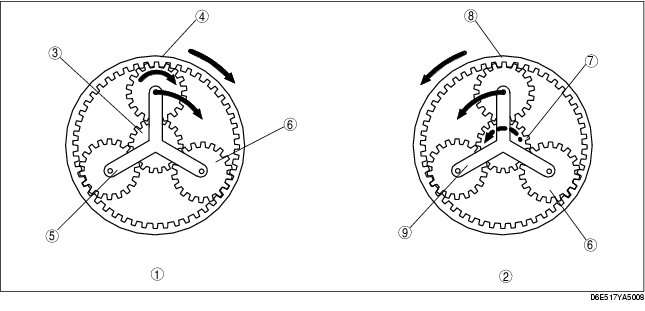
.
|
1
|
Rear planetary gear
|
|
2
|
Secondary planetary gear
|
|
3
|
Sun gear (fix)
|
|
4
|
Internal gear NRR (output)
|
|
5
|
Planetary carrier NCR (input)
|
|
6
|
Pinion gear
|
|
7
|
Sun gear NSS (input)
|
|
8
|
Internal gear NRS (input)
|
|
9
|
Planetary carrier NCS (output)
|
Gear rotation speed
|
Planetary gear
|
Rear
|
Secondary
|
|
Internal gear
|
NRR (output)
|
NRS (input)
|
|
Planetary carrier
|
NCR (input)
|
NCS (output)
|
|
Sun gear
|
0 (fix)
|
NSS (input)
|
• Suppose gear ratio in fifth gear is i5,
i5=NCR/NRR
• From the result of NSR=0 in formula (2), the relation between the gear ratio in fourth gear and the rotation speed of the rear planetary gear set is indicated in the following formula:
(ZRR+ZSR) NCR=ZRRNRR
Therefore,
i5=NCR/NRR=ZRR/ (ZRR+ZSR) =98/ (98+37) =0.7259
• Because the reduction ratio on the main shifting side is transmitted from the primary gear to the secondary gear, it can be calculated using the following formula:
The reduction ratio of the primary/secondary gear A = the number of primary gear teeth/the number of secondary gear teeth
Therefore,
A=82/86=0.9535
• Suppose the reduction ratio on the sub-shifting side is ii5,
ii5=NRS/NCS.
• From the result NRS=NSS in formula (1), the rotation speed of the secondary planetary gear unit can be calculated using the following formula.
(ZRS+ZSS)NCS=(ZRSZSS)NRS
Therefore,
ii5=NRS/NCS=(ZRS+ZSS)/(ZRS+ZSS)=(89+31)/(89+31)=1.000
And the reduction ratio of 5th gear= i5 x A x ii5=0.7259 x 0.9535 x 1.000=0.692
As a result, the reduction ratio of 5th gear is 0.692.
Reverse
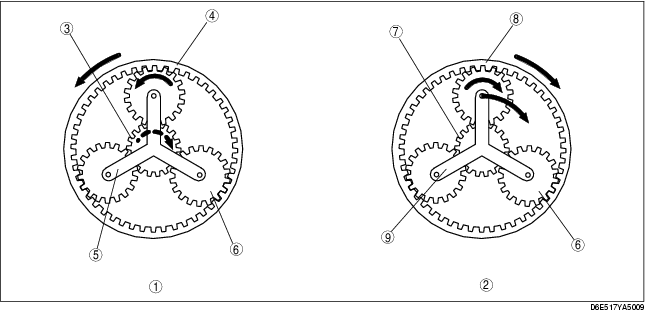
.
|
1
|
Rear planetary gear
|
|
2
|
Secondary planetary gear
|
|
3
|
Sun gear NSR (input)
|
|
4
|
Internal gear NRR (output)
|
|
5
|
Planetary carrier (fix)
|
|
6
|
Pinion gear
|
|
7
|
Sun gear (fix)
|
|
8
|
Internal gear NRS (input)
|
|
9
|
Planetary carrier NCS (output)
|
Gear rotation speed
|
Planetary gear
|
Rear
|
Secondary
|
|
Internal gear
|
NRR (output)
|
NRS (input)
|
|
Planetary carrier
|
0 (fix)
|
NCS (output)
|
|
Sun gear
|
NSR (input)
|
0 (fix)
|
• Suppose gear ratio in reverse gear is iREV,
iREV=NSR/NRR
• From the result of NCR=0 in formula (2), the relation between the gear ratio during reverse movement and the rotation speed of the planetary gar set is indicated in the formula below.
(ZRR+ZSR) 0=ZRRNRR+ZSRNSR
Therefore,
iREV=NSR/NRR=ZRR/ZSR=-98/37=-2.6486
• Because the reduction ratio on the main shifting side is transmitted from the primary gear to the secondary gear, it can be calculated using the following formula:
The reduction ratio of the primary/secondary gear A = the number of primary gear teeth/the number of secondary gear teeth
Therefore,
A=82/86=0.9535
• Suppose the reduction ratio on the sub-shifting side is iiREV,
iiREV=NRS/NCS.
• From the result NSS=0 in formula (1), the rotation speed of the secondary planetary gear unit can be calculated using the following formula.
(ZRS+ZSS)NCS=ZSSNRS
Therefore,
iiREV=NRS/NCS=(ZRS+ZSS)/ZRS=(89+31)/89=1.3483
And the reduction ratio of reverse gear= iREV x A x iiREV=-2.6486 x 0.9535 x 1.3483=-3.405
As a result, the reduction ratio of reverse gear is -3.405.







