PLANETARY GEAR OPERATION

BHE051319540A03

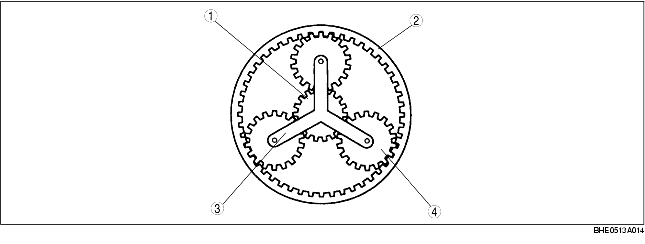
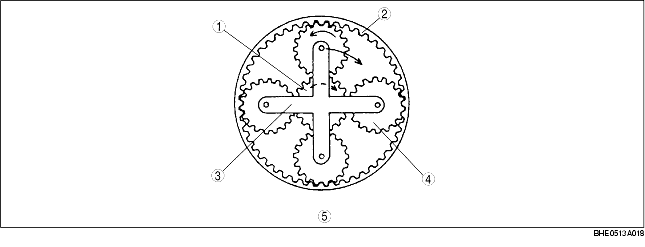
• The planetary gear works as a transmission when the sun gear and the internal gear are engaged.

• The sun gear, installed inside of the pinion gears, and the internal gear, installed outside of the pinion gears, are engaged with their respective gears. The sun gear and the internal gear rotate on the center of the planetary gear.


1	Sun gear
2	Internal gear
3	Planetary carrier
4	Pinion gear

• The pinion gears turn in the following two ways:

– On their own centers ("rotation")

– On the center of the planetary gear ("revolution")


1	Rotation
2	Revolution

Gear Ratio of Each Range

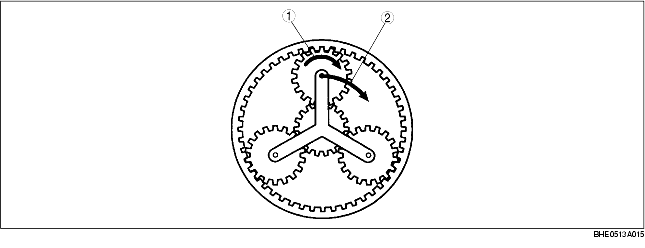
• The relation between each element of the planetary gear set and the rotation speed is generally indicated in the formula below.

(Z_R+Z_S) N_C=Z_RN_R+Z_SN_S--------------- (1)

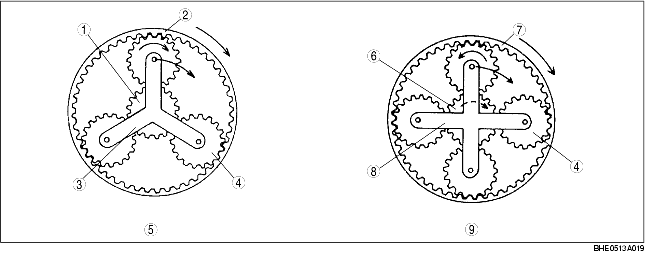
Symbol key

Z :

Number of teeth

N :

Rotation speed

R :

Internal gear

S :

Sun gear

C :

Planetary carrier (part of pinion gear)


1	Sun gear
2	Internal gear
3	Planetary carrier
4	Pinion gear

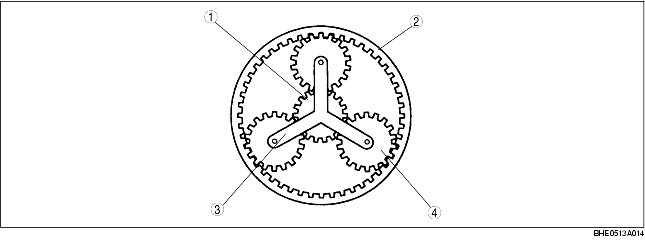
Number of teeth and symbol of each gear


Planetary gear		Number of teeth	Symbol
Front	Internal gear	75	Z_RF
	Planetary carrier (part of pinion gear)	21	Z_CF
	Sun gear	33	Z_SF
Rear	Internal gear	75	Z_RR
	Planetary carrier (part of pinion gear)	17	Z_CR
	Sun gear	42	Z_SR

Symbol key


1	Number of teeth of each element of planetary gear set
2	Front planetary gear set
3	Rear planetary gear set
4	Internal gear
5	Planetary carrier (part of pinion gear)
6	Sun gear

First Gear


1	Sun gear N_S (input)
2	Internal gear (fix)
3	Planetary carrier N_C (output)
4	Pinion gear
5	Rear planetary gear

Gear rotation speed


Planetary gear		Rear
Internal gear		0 (fix)
Planetary carrier		N_C (output)
Sun gear		N_S (input)

• Suppose the gear ratio in first gear is i₁,

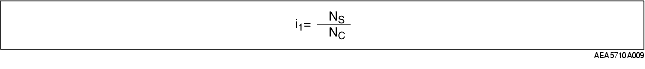
• From the result N_R=0 in formula (1), the relation between the gear ratio in first gear and the rotation speed of the planetary gear set is indicated in the formula below.

(Z_RR+Z_SR) N_C=Z_SRN_S

• Therefore,

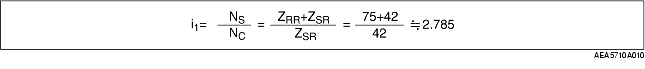
• As a result, the gear ratio in first gear is 2.785.

Second Gear


1	Sun gear (fix)
2	Internal gear N_R (output)
3	Planetary carrier N_C
4	Pinion gear
5	Front planetary gear
6	Sun gear N_S (input)
7	Internal gear N_R
8	Planetary carrier N_C (output)
9	Rear planetary gear

Gear rotation speed


Planetary gear	Front	Rear
Internal gear	N_R (output)	N_R
Planetary carrier	N_C	N_C (output)
Sun gear	0 (fix)	N_S (input)

Note

• The front internal gear and the rear planetary carrier are integrated.

• The front planetary carrier and the rear internal gear rotate at the same speed.

• Suppose the gear ratio in second gear is i₂,

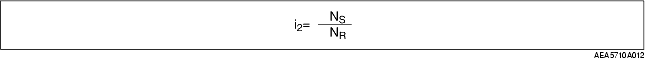
• From formula (1), the relation between the gear ratio in second gear and the rotation speeds of the front and the rear planetary gear sets is indicated in formulas (2) and (3).

(Z_RF+Z_SF) N_C=Z_RFN_R+Z_SFN_S--------------- (2)

(Z_RR+Z_SR) N_R=Z_RRN_C+Z_SRN_S--------------- (3)

• From the result N_S=0 in formula (2).

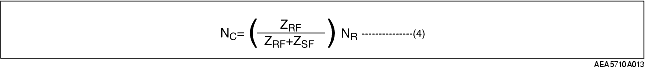
• Here we substitute formula (4) in formula (3).

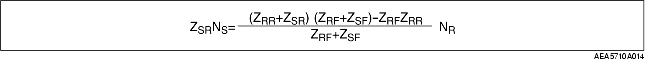
• Therefore,

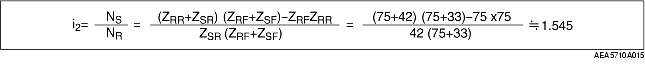
• As a result, the gear ratio in second gear is 1.545.

Third Gear


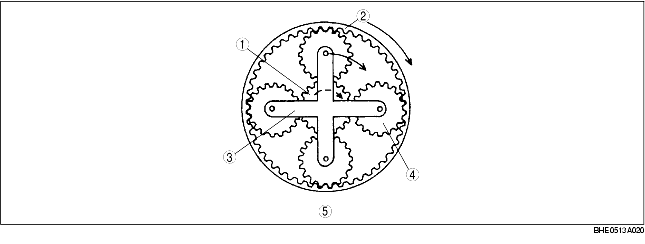
1	Sun gear N_S (input)
2	Internal gear (input)
3	Planetary carrier N_C (output)
4	Pinion gear
5	Rear planetary gear

Gear rotation speed


Planetary gear		Rear
Internal gear		N_R (input)
Planetary carrier		N_C (output)
Sun gear		N_S (input)

• Here we have the result of N_R=N_S.

• Suppose the gear ratio in third gear is i₃,

• From the result of N_R=N_S in formula (1), the relation between the gear ratio in third gear and the rotation speed of the rear planetary gear set is indicated in the formula below.

(Z_RR+Z_SR) N_C= (Z_RR+Z_SR) N_R

• Therefore,

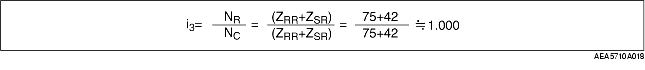
• As a result, the gear ratio in third gear is 1.000.

Fourth Gear


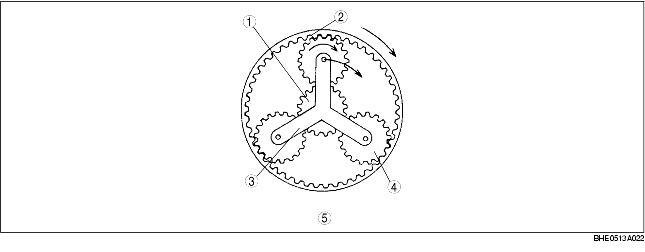
1	Sun gear (fix)
2	Internal gear N_R (output)
3	Planetary carrier N_C (input)
4	Pinion gear
5	Front planetary gear

Gear rotation speed


Planetary gear		Front
Internal gear		N_R (output)
Planetary carrier		N_C (input)
Sun gear		0 (fix)

• Suppose the gear ratio in fourth gear is i₄,

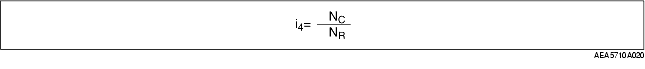
• From the result of N_S=0 in formula (2), the relation between the gear ratio in fourth gear and the rotation speed of the front planetary gear set is indicated in the formula below.

(Z_RF+Z_SF) N_C=Z_RFN_R

• Therefore,

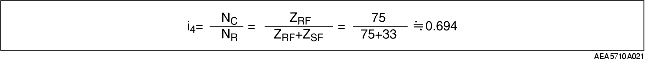
• As a result, the gear ratio in fourth gear is 0.694.

Reverse


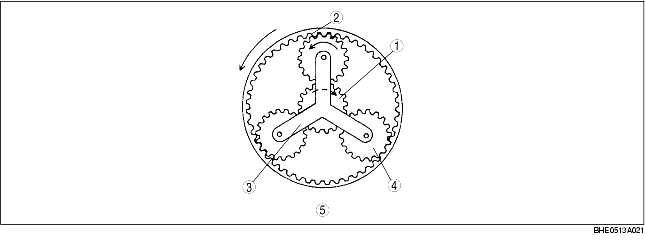
1	Sun gear N_S (input)
2	Internal gear N_R (input)
3	Planetary carrier (fix)
4	Pinion gear
5	Front planetary gear

Gear rotation speed


Planetary gear		Front
Internal gear		N_R (output)
Planetary carrier		0 (fix)
Sun gear		N_S (input)

• Suppose the gear ratio in reverse gear is i_REV,

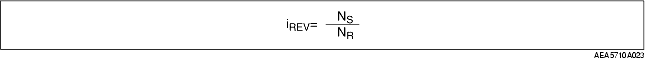
• From the result of N_C=0 in formula (2), the relation between the gear ratio during reverse movement and the rotation speed of the planetary gear set is indicated in the formula below.

(Z_RF+Z_SF) 0=Z_RFN_R+Z_SFN_S

• Therefore,

• As a result, the gear ratio in reverse is 2.272.